<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Lorsque l’on déforme un ressort ou un élastique, ces derniers réagissent en exerçant une <a href="/fr/eleves/bv/physique/les-forces-p1016">force</a> afin de reprendre leur forme initiale. </p>
</body></html>
On appelle force de rappel la force qu’exerce le ressort ou l’élastique pour reprendre sa forme initiale.
Les ressorts ne sont pas tous faits des mêmes matériaux et ne sont pas conçus de la même façon. Ils ont donc des propriétés différentes: deux ressorts différents sur lesquels on applique une force identique ne se déformeront pas de la même façon.
La constante de rappel est une propriété caractéristique des ressorts qui détermine la force qui peut être exercée sur un ressort pour qu'il se déforme sur un mètre.
Plus la constante de rappel est élevée, plus le ressort est rigide et plus il sera difficile de le déformer. Toutefois, plus cette constante est petite, plus le ressort est souple et plus il aura tendance à se déformer lorsqu'une force sera appliquée sur ce dernier.
Il existe une relation qui détermine la grandeur de la force de rappel en fonction de la déformation que le ressort ou l’élastique subit.
La loi de Hooke établit que pour un ressort idéal, la force appliquée par le ressort est égale à l’étirement ou à la compression du ressort multiplié par la constante de rappel du ressort.
La formule mathématique de la loi de Hooke est :
|F_{rappel} = - k \times \triangle x|
où
|F_{rappel}| représente la force de rappel |\small \text {(N)}|
|k| représente la constante de rappel |\small \text {(N/m)}|
|\triangle x| représente la déformation ou la compression du ressort (ou de l'élastique) |\small \text {(m)}|. Elle se calcule en effectuant la différence entre la position finale et la position initiale |(\triangle x = x_{f} - x_{i})|.
Certains éditeurs utilisent la variable |\triangle l| pour représenter le déplacement du ressort. Cette variable est la même que la variable |\triangle x| utilisée dans la formule écrite ci-dessus.
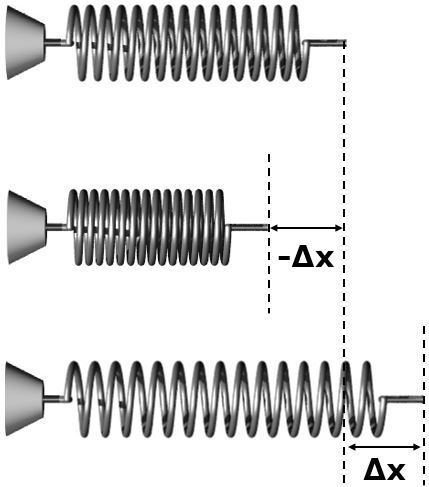
La déformation que subit un ressort peut être représentée de deux façons, soit par un allongement ou par une compression. Comme il a été mentionné dans la formule, la déformation est représentée par la différence entre la position finale du ressort et sa position initiale. L’illustration suivante représente ces deux cas.
Si un ressort est attaché sur un mur et qu'il est étiré vers la droite, il s'allongera également vers la droite. Cependant, le ressort va exercer une force vers la gauche pour reprendre sa forme initiale. Cette force est donc dans le sens contraire de l’étirement qu’il subit. C'est pourquoi il y a un signe négatif dans la formule: elle représente la force appliquée par le ressort. Si on cherche la force exercée sur le ressort, il faut ignorer le signe négatif de la loi de Hooke.
Il est possible de déterminer expérimentalement la constante de rappel d’un ressort en déterminant le taux de variation d’un graphique de la force de rappel en fonction de la déformation du ressort. Il suffit de déformer un ressort sur une distance prédéterminée et de noter la force nécessaire pour produire une telle déformation. Lorsque le ressort ne bouge plus, les forces sont équilibrées: la force de rappel du ressort est égale à la force appliquée sur le ressort pour le déformer.
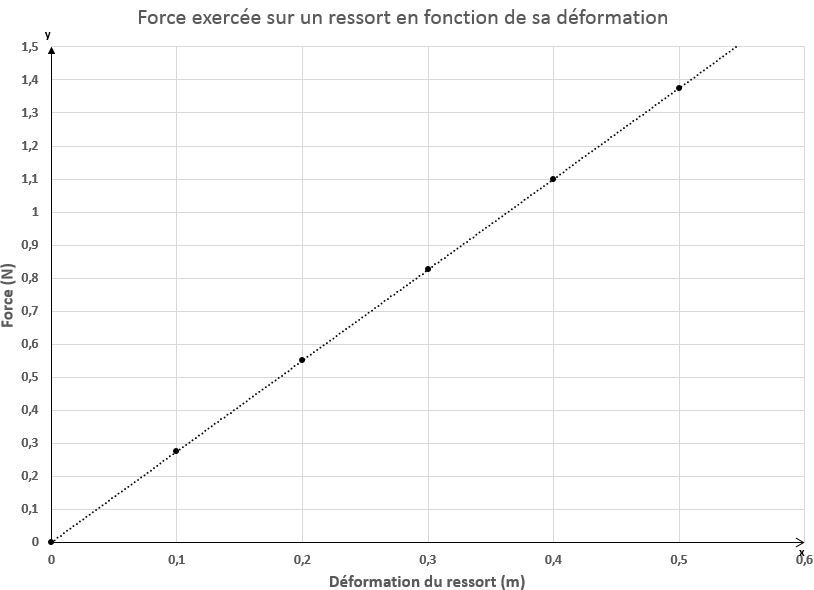
En déterminant le taux de variation de ce graphique, la constante de rappel du ressort peut être calculée.
||\begin{align}
k = \displaystyle \frac {Δy}{Δx} \quad \Rightarrow \quad
k &= \displaystyle \frac {(\text {1,1 N - 0 N})}{(\text {0,4 m - 0 m)}} \\
k &= \displaystyle \frac {\text {1,1 N}}{\text {0,4 m}} \\
&= \text {2,75 N/m} \\
\end{align}||
Ce taux signifie que si le ressort était déformé sur une distance d'un mètre, une force de |\small \text {2,75 N}| serait exercée par le ressort.
Une masse est accrochée sur un ressort dont la constante de rappel est |\small \text {15 N/m}|. Le ressort, qui avait une longueur initiale de |\small \text {10 cm}|, a maintenant une longueur de |\small \text {25 cm}|. Quelle sera la longueur finale du ressort si on lui accroche un objet qui a un poids de |\small \text {2,0 N}| ?
Dans le cas présent, la résolution du problème ne tiendra pas compte de l’orientation des forces et de l’allongement. C’est pourquoi le signe négatif ne sera pas inscrit dans l’équation de la loi de Hooke.
Il faut d'abord déterminer la force appliquée initialement sur le ressort. Les variables connues sont les suivantes.
||\begin{align} k &= \text {15 N/m} &x_f &= \text {25 cm = 0,25 m} \\ x_{i} &= \text {10 cm = 0,10 m} &\triangle x &= x_f - x_i = \text{0,25 m - 0,10 m = 0,15 m}
\end{align}||
Avec la loi de Hooke, il est possible de déterminer la force de rappel.
||\begin{align}
F_{rappel} = k \times \triangle x \quad \Rightarrow \quad
F_{rappel} &= \text {15 N/m} \times \text {0,15 m} \\
&= \text {2,25 N}
\end{align}||
La force de rappel sera égale à la force appliquée sur le ressort si le système est à l’équilibre, c’est-à-dire que le ressort ne bouge plus.
Il faut ensuite déterminer la longueur finale du ressort une fois le nouvel objet accroché. Les variables connues sont les suivantes.
||\begin{align} k &= \text {15 N/m} &x_f &= \text {?} \\ x_{i} &= \text {10 cm = 0,10 m} &F_{R} &= \text{2,25 N + 2,0 N = 4,25 N}
\end{align}||
Avec la loi de Hooke, il est possible de déterminer la force de rappel.
||\begin{align}
F_{rappel} = k \times \triangle x \quad \Rightarrow \quad
\triangle x &= \frac {\text {4,25 N}}{\text {15 N/m}} \\
&= \text {0,28 m}
\end{align}||
Pour calculer la position finale du ressort, il faut utiliser la variation dans le déplacement.
||\begin{align}
\triangle x = x_{f} - x_{i} \quad \Rightarrow \quad
x_{f} &= x_{i} + \triangle x \\
&= {\text {0,10 m + 0,28 m}} \\
&= \text {0,38 m}
\end{align}||
Le ressort aura donc une longueur finale de |\text {38 cm}| .
Plusieurs ressorts peuvent être associés entre eux. Des ressorts peuvent en effet être associés en série (1) ou en parallèle (2), comme illustré ci-dessous.
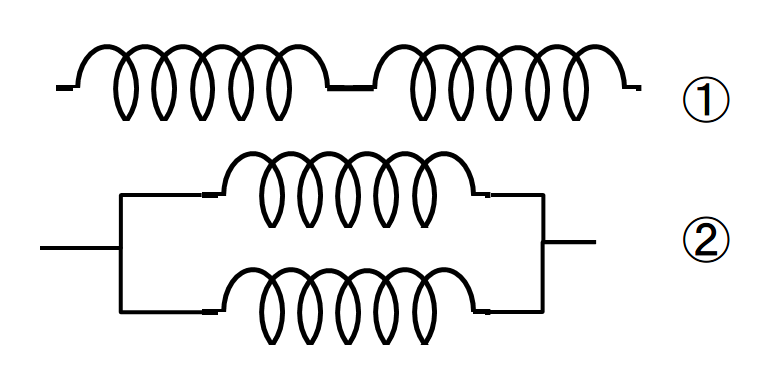
Dans ce cas, il est possible de les remplacer par un ressort unique.
(1) Ressorts en série
Lors d'une association de ressorts en série, l'inverse de la constante de rappel équivalente |k_{eq}| est égal à la somme des inverses des constantes de rappel spécifiques à chacun des ressorts.
||\frac{1}{k_{eq}} = \frac{1}{k_1} + \frac{1}{k_2} + \ldots + \frac{1}{k_x}||
(2) Ressorts en parallèle
Lors d'une association de ressorts en parallèle, la constante de rappel équivalente |k_{eq}| est égale à la somme des constantes de rappel spécifiques à chaque ressort.
||k_{eq} = k_1 + k_2 + \ldots + k_x||